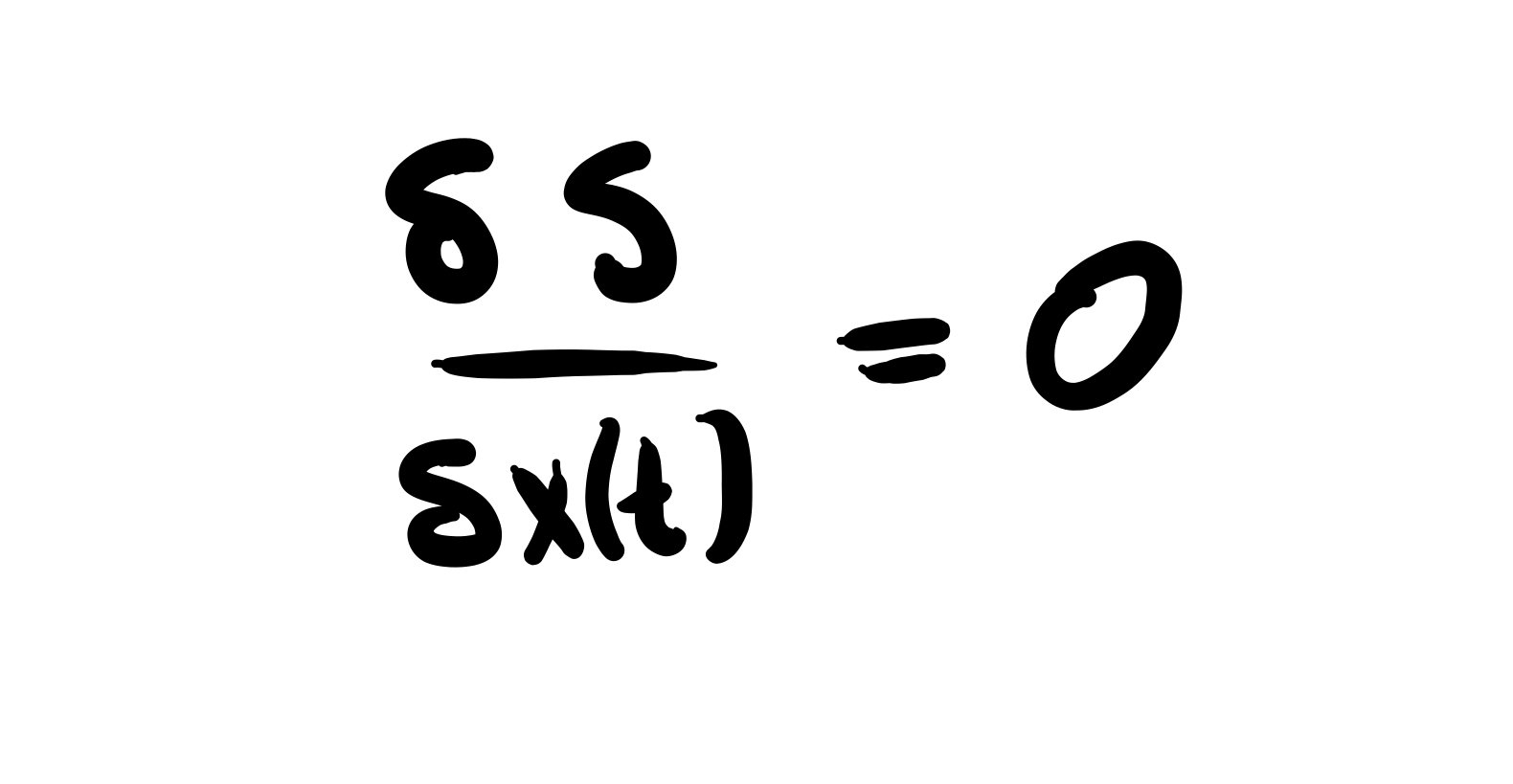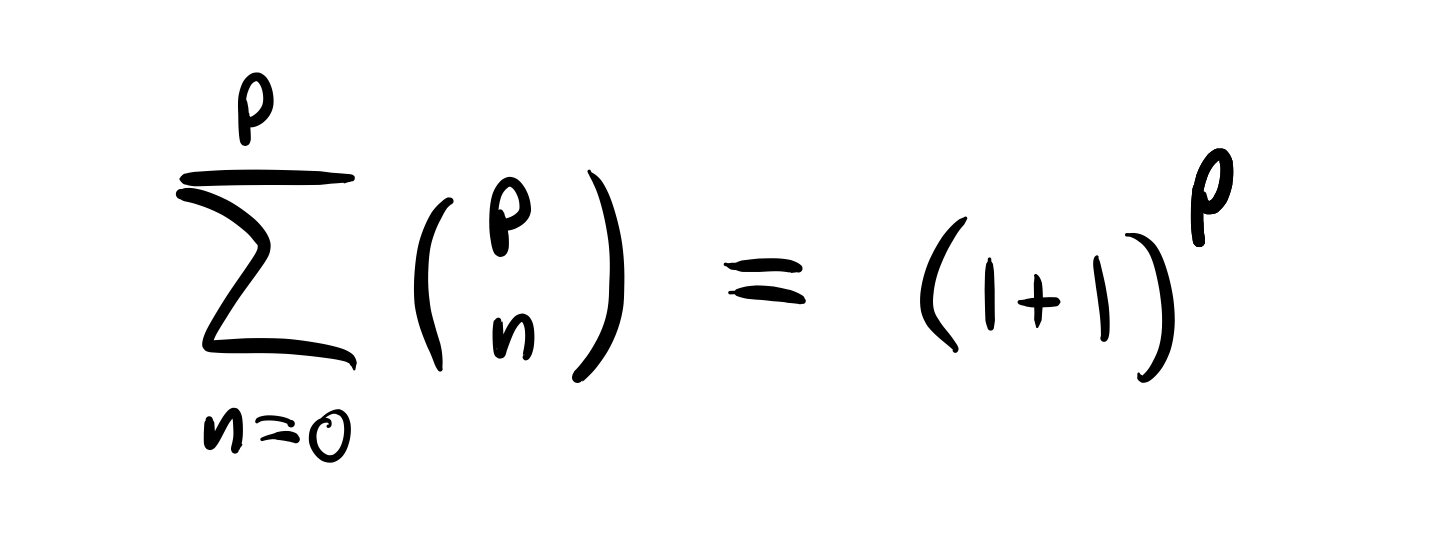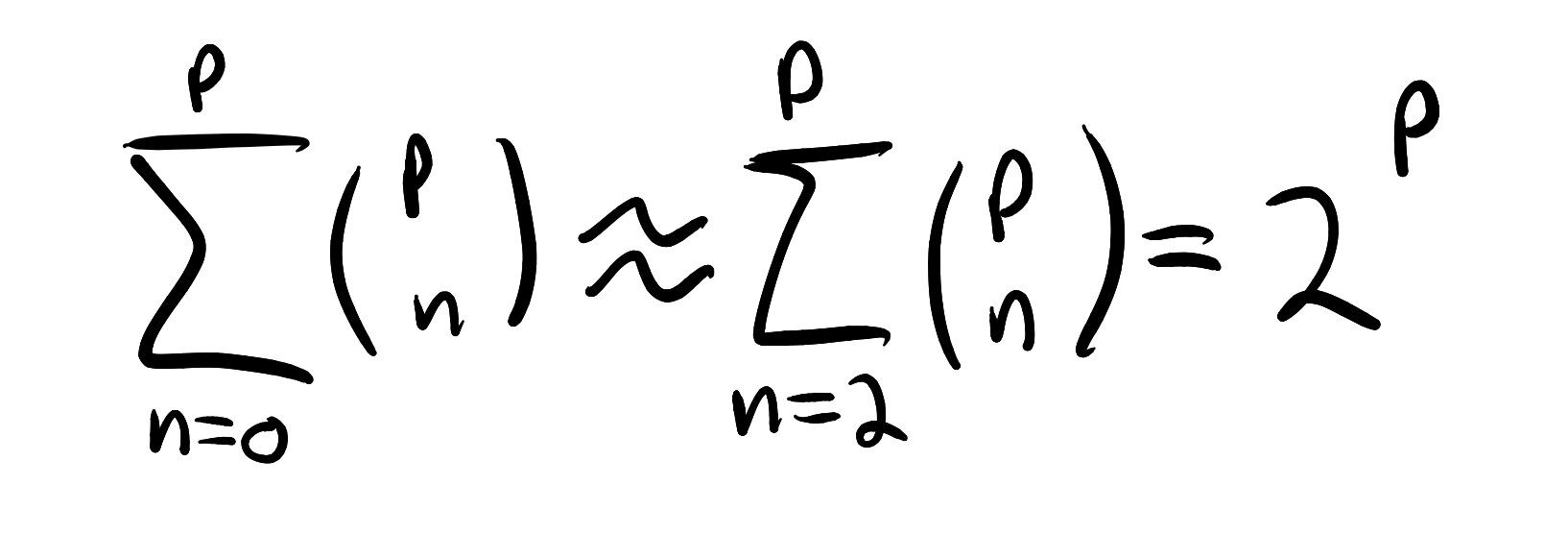Poker Bot
Together with my friends (and fellow UW grad students) Charles Cardot, Mikael Kovtun, and John Stroud, we entered a competition to put together a poker bot, which was supposed to compete against other poker bots.
Although the competition fell through, we put together a pretty respectable and scrappy little bot, which featured several strategies, and a protocol for switching between them depending on how the bot was performing. The most sophisticated strategy was a simplified version of counterfactual regret minimization, which was primarily implemented by Charles, and which we called “killer bot”. Mikael was primarily responsible for building a C++ poker engine for testing and parameter-optimizing our bots. My contribution was to build a set of “heuristic bots”, which used monte carlo hand sampling and simple rules of thumb (e.g., “raise if your probability of winning exceeds 0.6”, “go all in every time”, etc.). These simple bots, variously called “fish bot”, “shark bot”, “all-in bot”, etc. were valuable to have as a benchmark to beat for the more sophisticated killer bot, and required some simple parameter optimization to get in working order.
For full details, see Charles’ blog: https://charlescardot.github.io/2024-05-04-Poker-Bot/
The awesome artwork above is due to John. Below on the left is Mikael, myself, and John. On the right is Charles, excited about the next project from the Computational Physics Journal Club, and who took the picture on the left.