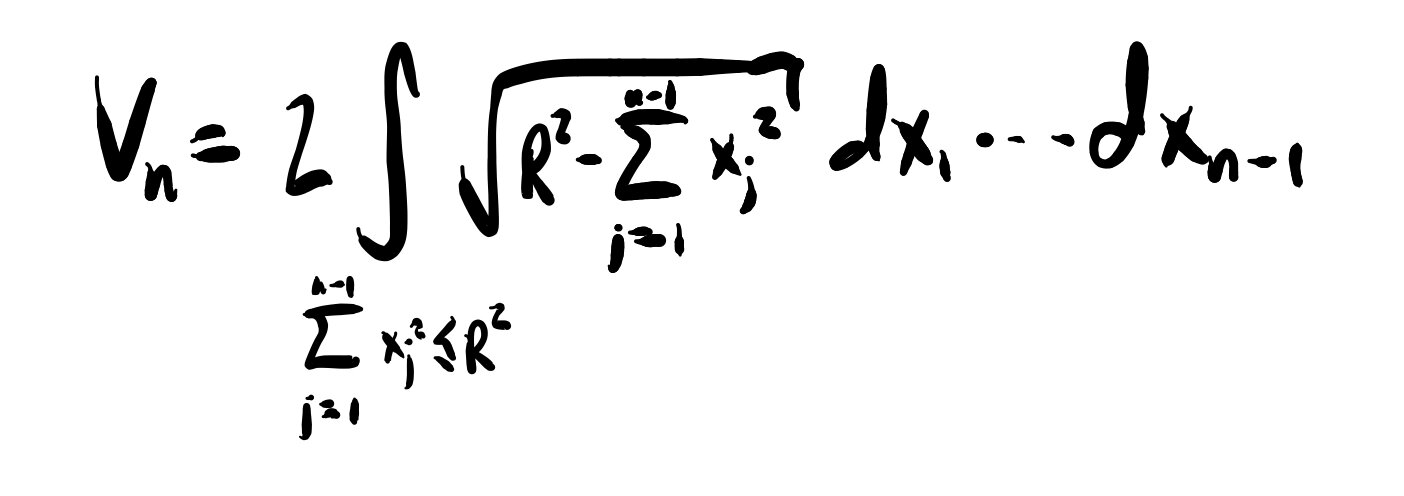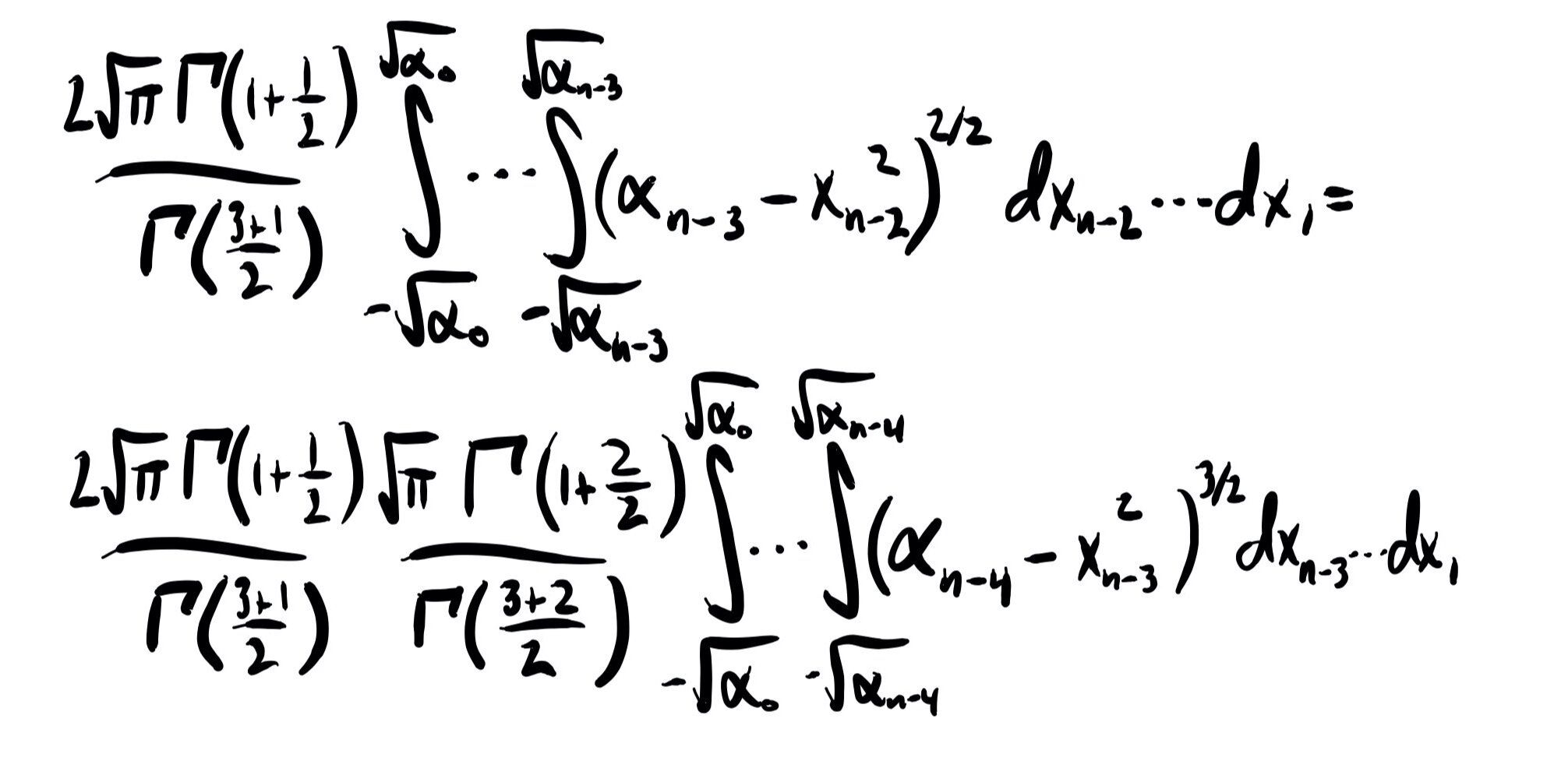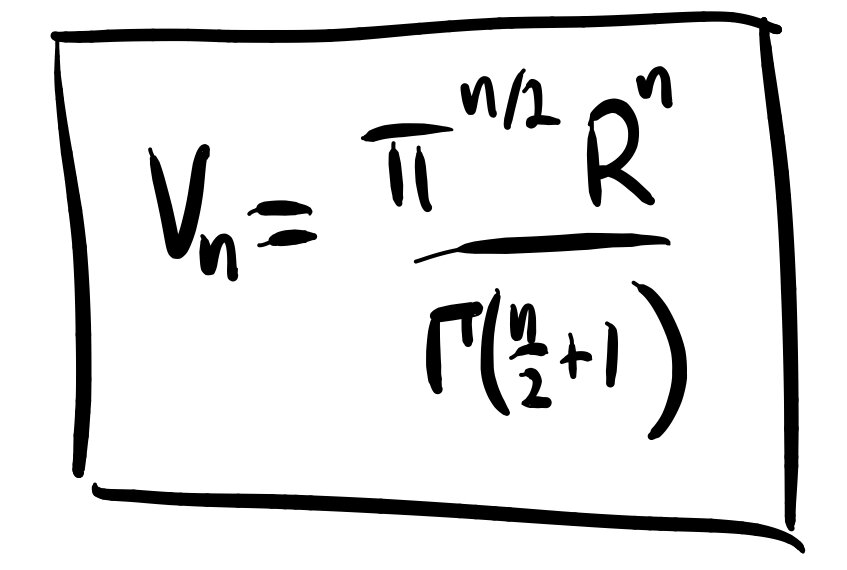Volume of Spheres in Higher Dimensions

Hi everyone,

Today I will be deriving the formula for the volume of a sphere in any dimension. This is nothing new mathematically speaking, but it is exciting to me because I re-derived the results myself! Let’s get started.

Derivation

We define a sphere in n-dimensions as follows:

We wish to compute the volume of this n-sphere, which amounts to computing the following integral:

However, it is not immediately clear to me how to compute this integral given the irregular domain. Instead, we express the sphere as a function, and integrate this function to discover its volume. We choose the nth coordinate to be our function. That is,

Note that we are now interested in the surface of the n-sphere, and we will integrate to find the volume enclosed by this surface.

One issue that immediately presents itself is that this function is multivalued. We can address this in two ways. We could perform two integrals to get the volume enclosed by the positive part of the surface and the negative part of the surface respectively. Alternatively, we could recognize the symmetry between the positive and negative surfaces, find the volume underneath one of these surfaces, and then multiply our final answer by two. We choose the positive surface for convenience. Thus, we have

Next, we must determine the bounds of this integral. They are going to be pretty ugly, given that we are still using cartesian coordinates. But we can at least write down the integrals somewhat easily in cartesian coordinates, and it turns out that we will actually be able to compute them with a little help from Mathematica.

Crucially, we observe that xn is now a function defined on the domain of {x1, …, xn-1}. That is, we are now integrating x_n over the (n-1)-sphere:

At this point, I am going to take a second to define some notation. We are going to be writing expressions that look like what’s underneath the radical a lot, so let’s use the following shorthand:

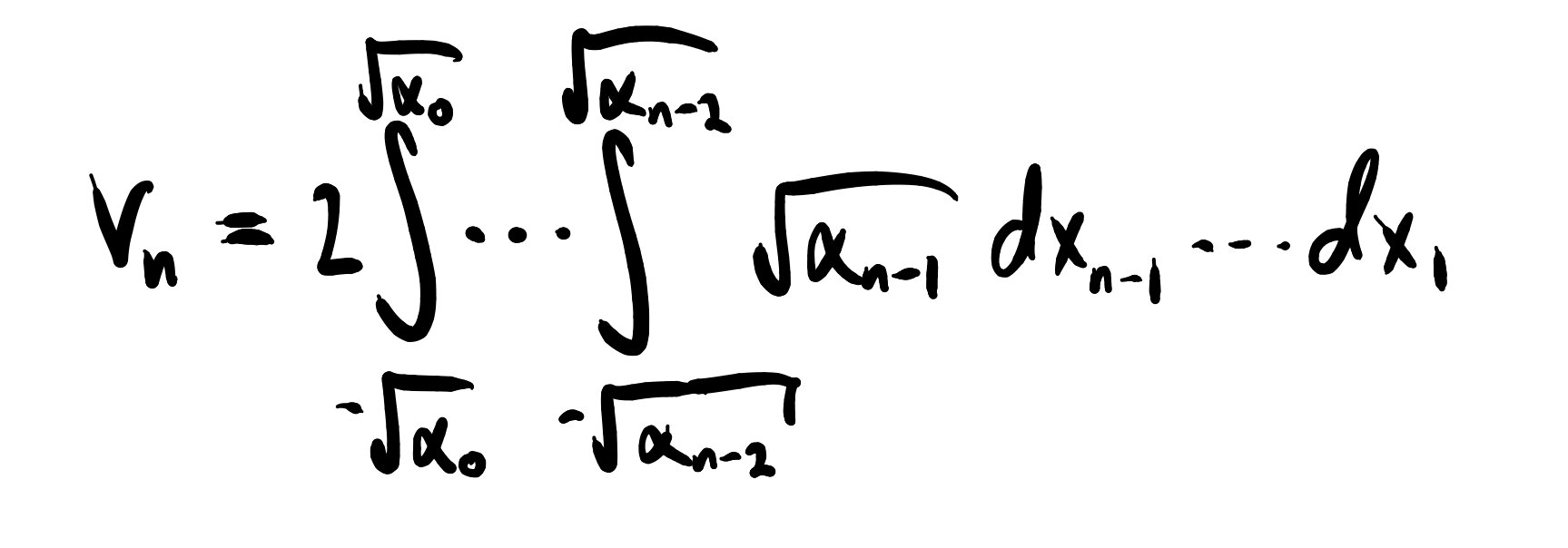
Next, we have to figure out the bounds of our integrals. We first integrate over the (n-1)-th variable. At this point, we have not constrained any of our other variables. So we will be integrating from one edge of the (n-1)-sphere to the other, which I claim amounts to

I hope it is becoming clear why we introduced alpha. We next integrate the (n-2)-th variable. So far, we have integrated out x_n-1, but all the other variables remain to be considered. By the same logic, integrating the next variable across our (n-1)-sphere gives

At this point, the pattern becomes clear. We simply continue this procedure until we have integrated over all our variables. We are now in a position to write down the full integral for the volume of a sphere in n-dimensions. Remembering our factor of 2 from earlier, we have

Okay, it’s worth pausing at this point. This integral is very ugly, especially when we remember how much complexity we have subsumed into those alphas. Nevertheless, we now have a definite integral which contains our answer. If we can compute that integral, then we will have a general formula for the volume of a sphere in any dimension.

Well, it turns out that we actually can compute this integral, and we only need one result to do so. The result we need is as follows:

Now, let’s start working on our big nasty integral.

Here, we can start to see a pattern emerge. We will integrate each variable out one by one, each time acquiring a coefficient on the outside of the integral that depends on the exponent of the integrand, m. How long does this pattern continue? Until we run out of integrals. Since we integrate over n-1 variables, we will end up with coefficients

Given that each integral simply increments the exponent on alpha by 1/2, we only need to evaluate the final integral to get our result:

In fact, we already included the pi and gamma terms in the product we computed above, so all that we were missing was R^n. Finally, putting everything together, we derive the formula for the volume of a sphere in n-dimensions!

Results and Discussion

I don’t blame you if you got lost in the above derivation. It certainly wasn’t the most elegant thing I’ve ever calculated. So I would like to make a few remarks on why I did it this way.

First of all, you may ask why I used cartesian coordinates to compute a result about spheres. And the answer is that I certainly tried to derive higher-dimensional spherical coordinates. I was able to derive the correct coordinates for dimensions 4 and 5. However, I was unable to come up with a systematic way of determining how the new angles I introduced were parameterized. Did they run from 0 to π? 0 to 2π? Did it vary based on the dimension? My naïve attempts to answer these questions gave me nonsense results for the volumes, so I had to find another way.

Second of all, you may ask why this was worth doing in the first place. This is a lot of calculus with a lot of square roots. What is the payoff? I claim that there is actually a big payoff for all that hard work. Let’s take a look at how the volumes of unit spheres (i.e. R=1) vary as we increase the dimension:

I don’t know what you were expecting, but I think that curve is astonishing. Who would have guessed that it would have a peak? It turns out that 5 dimensional unit spheres have the most volume! Naively, I would have guessed that they just kept getting bigger as you increase the dimension. And not only do they not keep getting bigger, but it is easy to verify that

Given that spheres are in some sense the simplest shape one can consider, it is clear that higher dimensions have many surprises in store indeed.