Infinisecting & Exotic Shapes
Hello everyone,
I wanted to share with you a quick math puzzle today. I had fun working it out, and maybe you will enjoy looking at it. I hope that maybe someone else decides to try this because it seems like there could be an enormous diversity of solutions to this puzzle, and I could only really come up with a few! (Please leave any solutions you come up with in the comments!)
Puzzle: Construct a compact shape in two dimensions such that, if you cut through the shape in a straight line, you divide it into an infinite number of pieces. Let us call this cut an “infinisection” of our shape.
To get a feel for what I’m talking about, consider the following simple examples. We can trivially divide a compact line segment and a circle into two pieces by cutting through each with a straight line:
It is also not difficult to conceive of shapes which could be cut into a very large number of pieces:
You could imagine extending this for 100 miles. Or a million. So long as you stop somewhere, since the shape just must be compact. But since we are stopping somewhere, shapes like this will always be cut into a finite number of fragments.
So again, the puzzle is to come up with some compact shape such that if we apply the procedure above, it is cut into an infinite number of pieces. Intuitively, it seems like such a shape is going to have to do a lot of oscillating or folding or doubling back on itself if it is going to fit an infinite amount of waving in a finite space.
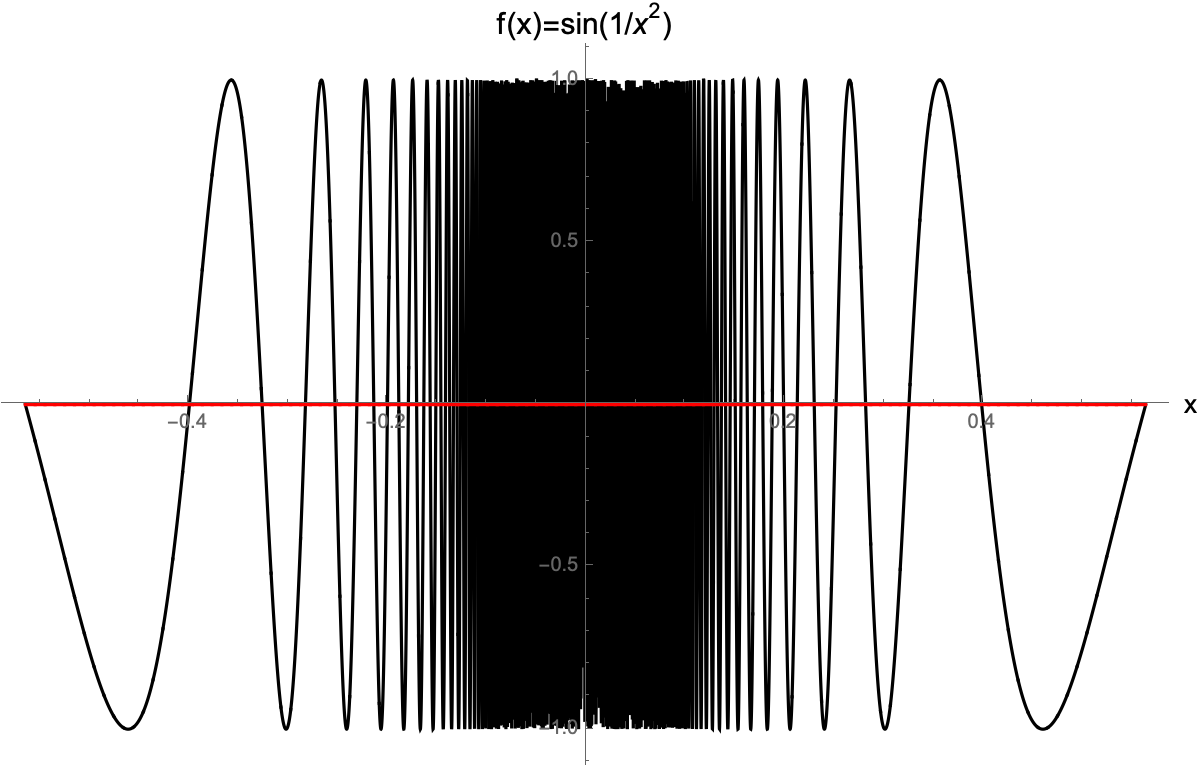
And in fact, we can construct a solution by looking for examples of things that oscillate an infinite number of times within a finite space. One such shape is the curve traced out by the function
The zeros of this function occur when
(restricting ourselves to the reals). We must truncate the curve somewhere to ensure the compactness of the shape. Without loss of generality, we truncate the curve at ±x1 = ±1/sqrt(pi). Does this curve in fact oscillate an infinite number of times between the endpoints we have specified? Yes!
Since there is an infinite number of natural numbers n, there will be an infinite number of xn’s in our interval.
Now that we have a curve which oscillates an infinite number of times in a finite space, it is simple to choose a line that infinisects it: simply choose the line f(x) = 0. That way, the curve gets cut at each of its zeros, and the pieces are the nonzero parts of the function between those zeros!
Well, there we are. This is at least one example of a compact shape that can be cut into an infinite number of pieces with a straight line. Can we construct others?
Yes, it is actually not too difficult to do so. We can use many functions and curves that have some periodicity to them to accomplish what we accomplished above. We could imagine making trivial changes to the curve above which preserve its essential structure:
So, once we have one solution, it is fairly easy to construct an arbitrarily large number of other solutions. However, none of these is really more interesting than the original.
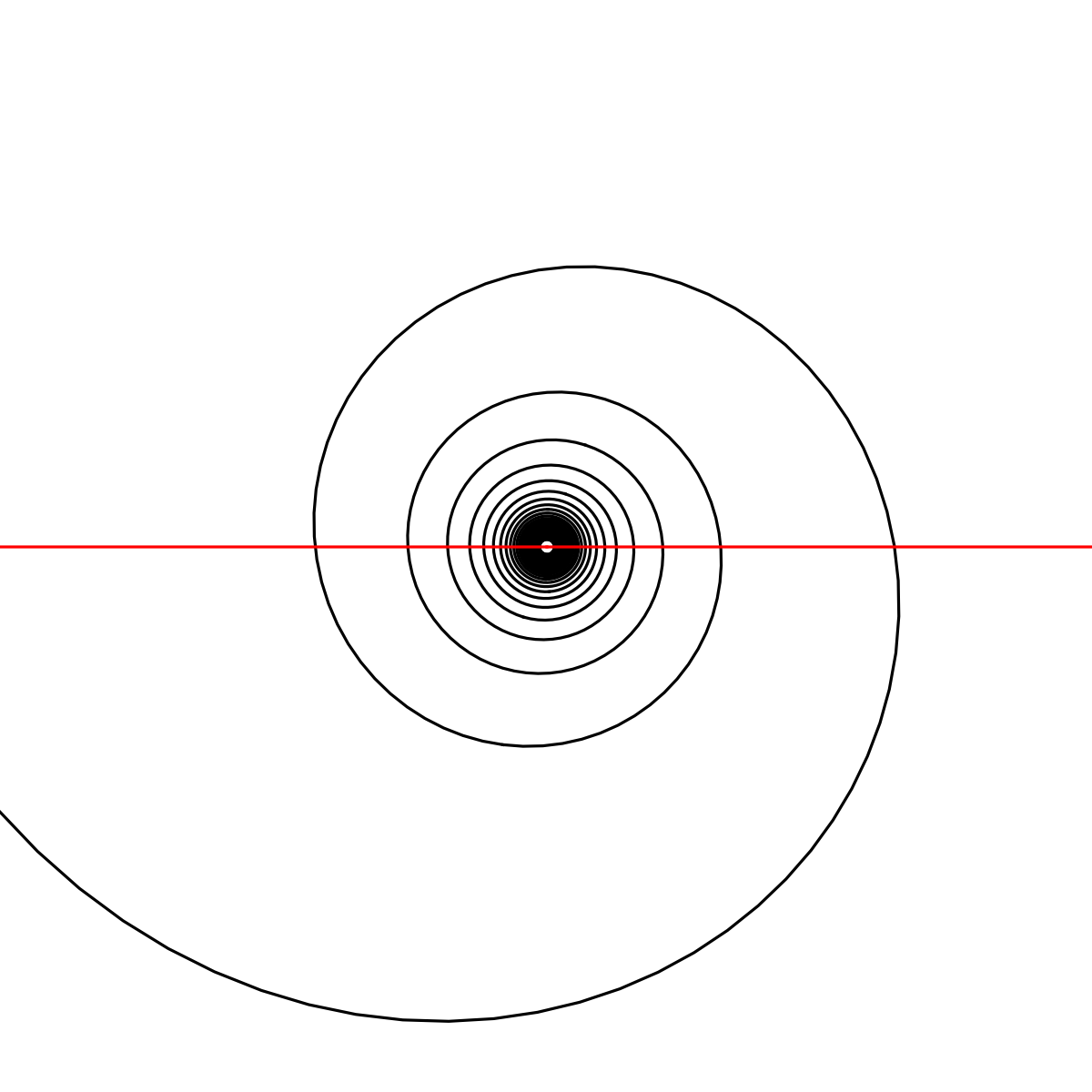
A slightly more interesting example is that of an asymptotically decaying spiral
which we could parameterize with something like
This is a bit unsatisfying since we have in some sense made our shape non-compact in its parameterization (i.e. t is unbounded), but we can prove that does the job all the same.
So far, we have found many shapes which can be infinisected by straight line. However, all the shapes that we have considered above have been highly regular: they each essentially have some periodicity and some asymptotic acceleration which allow them to fit an infinite curve into a finite amount of space. But I can’t think of any reason why there shouldn’t be just as many––probably far more––irregular shapes which also solve our puzzle. This is where the puzzle gets much more interesting, and far harder. Beyond this point I can only make educated guesses.
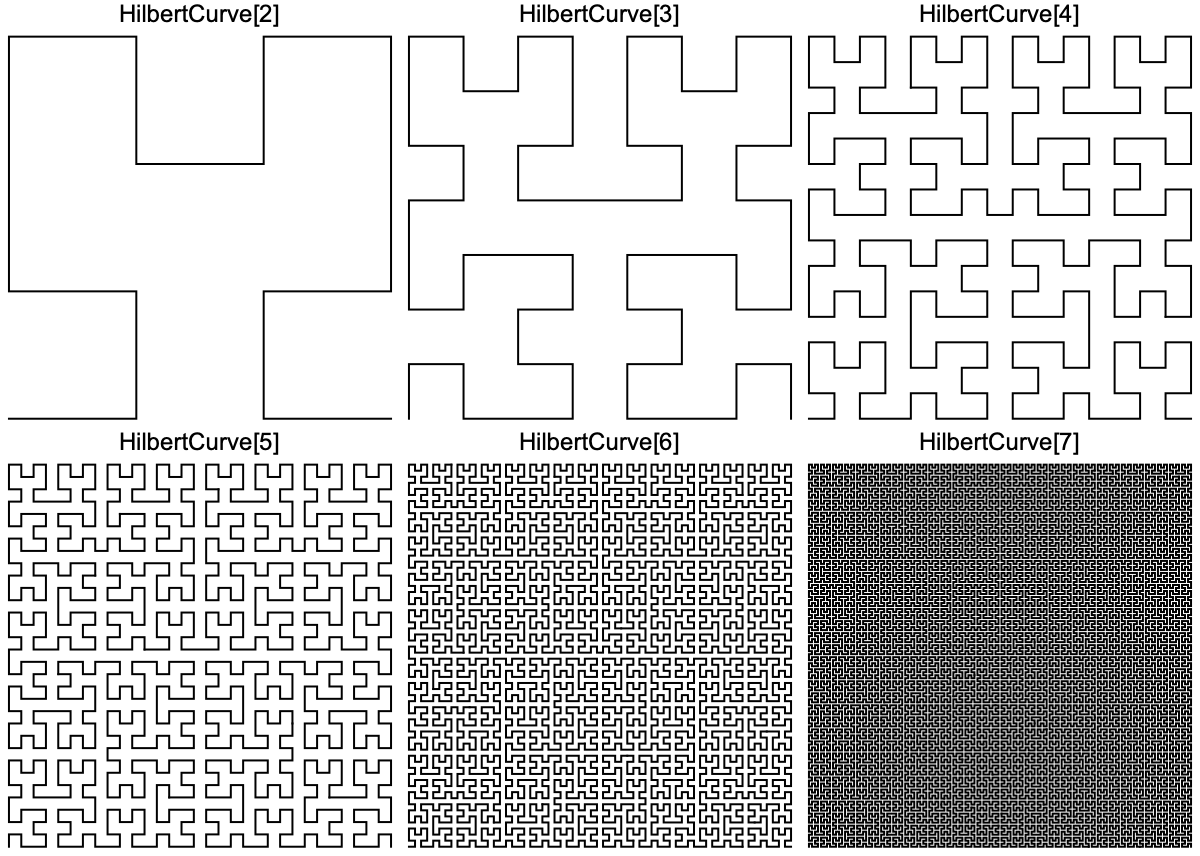
We may be able to construct one such “irregular” example from a space filling curve such as a Hilbert curve. A Hilbert curve is a continuous one-dimensional curve which weaves through space in such a way that it touches every point in some two-dimensional region exactly once. It is constructed by taking the limit of curves which look like this:
The Hilbert curve is clearly an object of far greater complexity than those we were considering before, and its true form is far harder to visualize as well. A 1D curve that manages to touch every point in this square once while remaining continuous is clearly an object with many unfathomably dense twists and turns in it. But it is not clear whether the curve twists in just such a way that a straight line will in fact infinisect it.
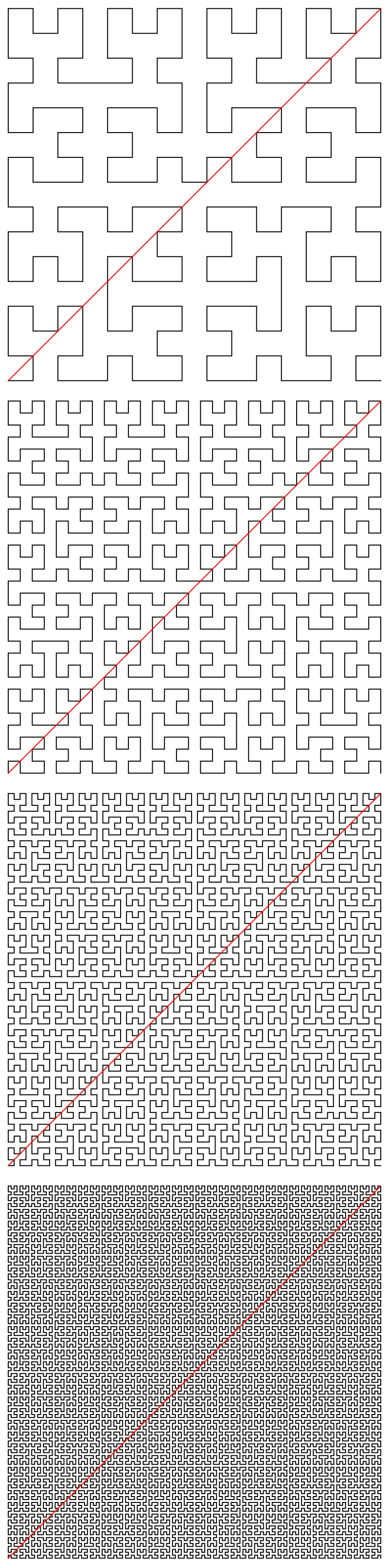
Let’s take a look at diagonal cuts of these proto-Hilbert curves
Looking carefully at these images above, we can see that a diagonal line does indeed appear to cut each proto-Hilbert curve into a number of pieces. It appears that we may be able to estimate the number of pieces that the proto-Hilbert curve forms by counting the number of intersections between the curve and the diagonal line.
If this approximation is valid, we may be able guess the behavior of the true Hilbert curve by looking at how the number of intersections scales as we increase the index of the proto-Hilbert curve. This is easy enough to check in Mathematica, and we observe
So the number of intersections does appear to be increasing with n (although, since the Hilbert curve is defined recursively, these computations quickly become intractable and difficult to check for n > 12). Does this mean that the true Hilbert curve is actually infinisected by the diagonal line? If I had to guess, I would guess that the answer is yes. But this is far short of a proof, and I have almost no idea how I would go about proving such a thing formally.
And if Hilbert curves solve our puzzle, what else does? Hilbert curves are not the only space-filling curves around. What about Peano curves?
I am not well-versed in the math of space-filling curves, but I am sure there are an infinite number of them. It would be very interesting to learn about the kinds of space filling curves which can be infinisected. Because the space filling curves that we have considered, exotic though they undoubtedly are, still have a sort of “regularity” to them. It is exciting to ponder what sort of bizarre, pathological, monstrously irregular (space-filling) curves might live out there in the Platonic world which could be infinisected if anyone could ever describe them.
A bizarre, pathological, monstrously irregular (approximation to a) space-filling curve.
At this point though, I have stepped far beyond my domain of expertise, so I will leave the post here. I hope you found this puzzle fun to think about. And again, if you can come up with other solutions, please post them in the comments! I would love to hear what people come up with.
Until next time, be well and be safe.
-Matt