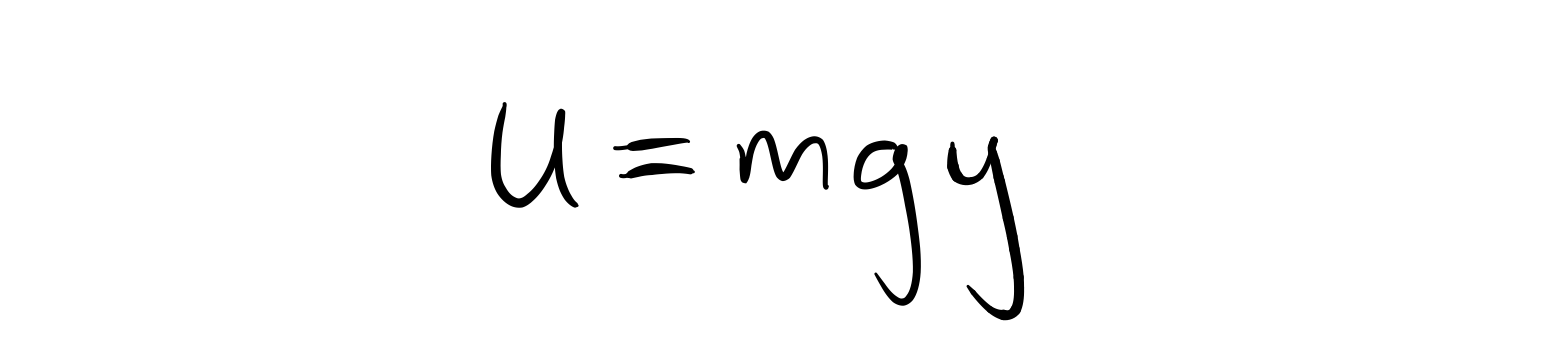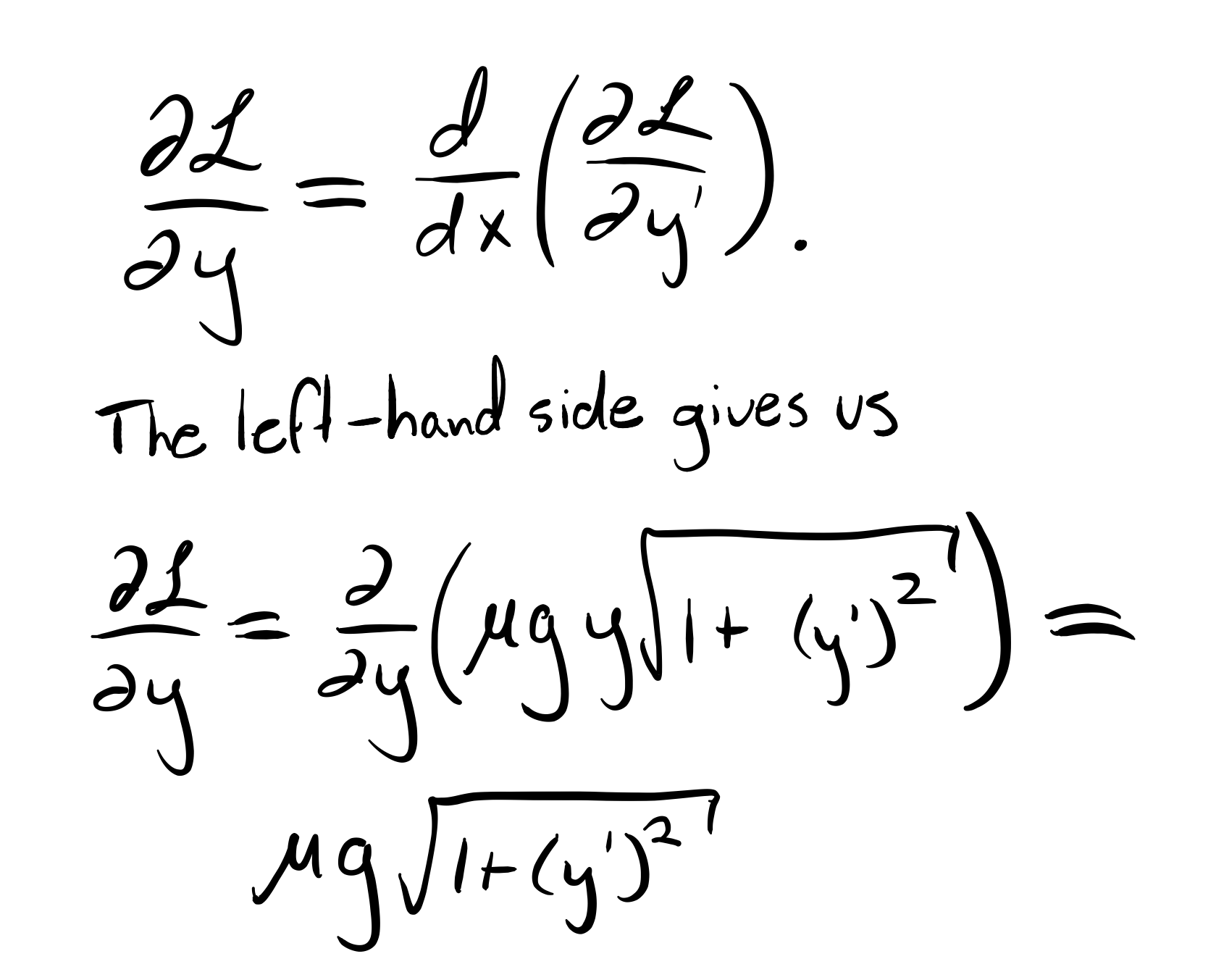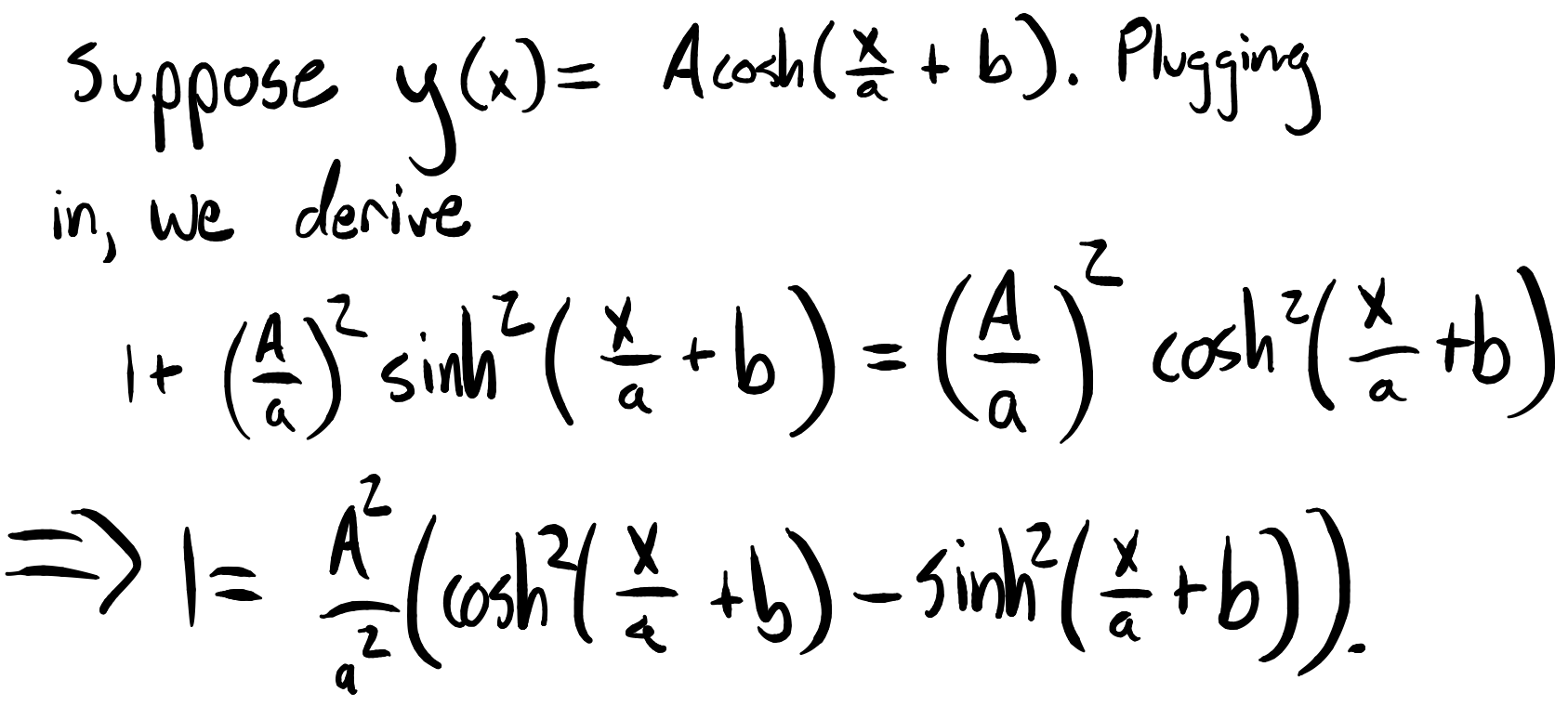Functional Approach to the Catenary Problem
In this post, we will solve a famous problem in the history of physics: what shape does a chain take when it is hung between two posts?
In order to address this problem, we will make use of a so-called “functional” approach. That is, we will assign a functional for the potential energy of hanging chain, and we will try to find the shape of the chain that will minimize that energy.
First of all, we must define what a functional is. Simply put, a functional is a function which takes another function as its argument and returns a number. In this case, the function we are going to be using as our input will be the shape of the chain, y(x). Then, the functional will be a function that takes that shape function, and returns the chain’s potential energy. The fundamental question we wish to solve is: for which configuration of the chain, y(x), is our potential energy functional the smallest?
First, we must figure out how to write our functional in the first place. Typically, the gravitational potential energy of an object can be expressed simply as
However, we usually use this formula to describe the potential energy of a localized mass. In this case, we want to describe the potential energy of a spatially extended shape. So, what we will do instead is assign a potential energy for an infinitesimal segment of the chain, dU, and then integrate this over the length of the chain.
How can we find dU? We can get from the potential energy to an infinitesimal potential energy by replacing a point mass with an infinitesimal mass dm. We also change from y to y(x), to allow the height of the chain to vary from point to point along the chain.
If we wish to integrate over the length of the chain, we must then change our differential to be in terms of arc length along the chain. In this case, dm becomes
where mu is the mass per unit length along the chain (which we assume to be uniform), and ds is an infinitesimal segment of arc length.
Putting this all together, we finally have an expression for the total potential energy of the chain. Suppose that our posts are located at x = -L/2 and x = L/2. Then, the chain’s potential energy is given by
As a sanity check, is this actually a functional? Yes it is! It takes a function y(x) as an argument, and returns a number. So far so good.
At this point, we should pause and celebrate what we have done so far. It was not trivial to come up with this expression, and now that we have it, we are much closer to solving our problem. On the other hand, it appears that we have just hit a huge wall. We recall that our original goal was to find a configuration of the chain, y(x), that minimizes our potential energy functional. Taking a close look at this equation above should reveal that this is not such a simple thing to do.
At first we might propose simply taking a derivative of U with respect to y, and setting the result equal to 0. However, y(x) is an entire curve, not simply a variable. So the standard tools of calculus won’t be able to help us here. Luckily, there is technique from a branch of math known as the calculus of variations which allows us to sensibly take a derivative of U with respect to the entire function y(x). This operation is known as the variational derivative of U, or alternatively the functional derivative of U, and is denoted
So, we have now recast the catenary problem in terms of an equation involving a variational derivative: the configuration of the chain, y(x), which minimizes the potential energy U can be found by solving the equation
All that remains is figuring out how to solve this equation. Luckily, this is not so hard. All we need is one very important result from the calculus of variations.
Theorem: Suppose that we have a functional U, which is expressed in the following form
where script-L (often called the Lagrangian) is simply a function of x, y(x), and dy/dx. Then, the function y(x) which minimizes U with respect to y satisfies the Euler-Lagrange Equation:
It would take us too far out of our way to go through a proof of this theorem here. You can find one on the Wikipedia page, which I linked to above, if you are interested. In any case, proving this theorem is not necessary for understanding and using it. And this is a very important result in physics. Because many, many problems can reformulated in terms of minimizing functionals. And once we have done that, all we have to do is use this theorem, and then we can find their solutions.
So let’s find the catenary curve!
If we compare the general formula given in the theorem with the specific one that we derived, we see that our Lagrangian is given by
Given that we wish to minimize the potential energy with respect to y, we must now plug into the Euler-Lagrange equation. Doing so will allow us to find y(x). What follows is a lot of messy calculus, so strap in.
It is important to note here that, when solving the Euler-Lagrange equation, y and y’ are treated like two entirely separate variables! This is why the square root term is not affected by this partial derivative.
(I forgot my mu • g! I will put it back I promise.)
We now equate the two sides of the Euler-Lagrange Equation, put back the mu and g where they are supposed to go, and get
Whew! Okay, let’s take a breath, and examine what we got. That was certainly a mess, but it was really just taking a few particularly nasty derivatives. Now that we have done so, we are left with a differential equation for y. If we can solve that differential equation, we will have found the shape of our chain, at long last.
Unfortunately, this equation is nonlinear, so you won’t get anything nice by simply plugging into your favorite differential equation solver. However, it is not too difficult to simply guess what a nice solution might be, and see what we get. If you throw solutions against the wall for long enough, you might propose the following:
Lastly, we recall that we imagined our chain to be hung between posts at x = -L/2 and x = L/2. As a result, the chain will be symmetrical about x = 0. Since cosh(y) is symmetrical about x = 0, we conclude b = 0. Thus, we arrive at our final answer:
(Interjection from future Matt!!! You might, like me, have found the solution to the differential equation above a bit unsatisfying. I was not up to the task of solving it myself, but my good friend Jeremy Welsh-Kavan found and wrote up a great solution. Check it out here.)
This is known as the catenary curve! Below, I have plotted the catenary curve for different values of a, with the fence posts at x = ± 3.
The last thing that remains is to compare it with a real hanging chain.
Not a bad fit!