Exploring the Central Limit Theorem Computationally
Hello everyone! Welcome to Stochastic Tinkering :)
Today, I would like to write a bit about the Central Limit Theorem.
I have taken several courses in the past in which I was taught the Central Limit Theorem, but it has never quite made sense to me. However, in a conversation with Stephen Wolfram at the 2021 Wolfram Summer School, Nassim Taleb provided a Mathematica demonstration which allowed me to understand the Central Limit Theorem better than I ever have before. In what follows, I have tried to reproduce what I was able to understand from Dr. Taleb’s presentation. All credit for brilliance goes to Dr. Taleb, and all errors are my own.
I hope that you will find the demonstration as valuable as I did.
Roughly speaking, the Central Limit Theorem says that sums of independent, identically distributed random variables will themselves tend to be normally distributed, regardless of the underlying distribution of the random variables. When stated like this, I have to think very hard to understand what the CLT is actually saying. But Taleb’s demonstration makes things much clearer.
First, let’s get some random variables. We’ll start with a uniform distribution on the interval [0, 1].
This is what is meant by “independent, identically-distributed random variables.” We are just sampling our distribution over and over again, and we end up with a bunch of values between zero and one. Now, we sum them up. In this case, the sum is equal to 44.9921.
We do not have any reason to care about the particular value of 44.9921 by itself. However, a pattern emerges if we repeat this procedure above many times and compare the results.
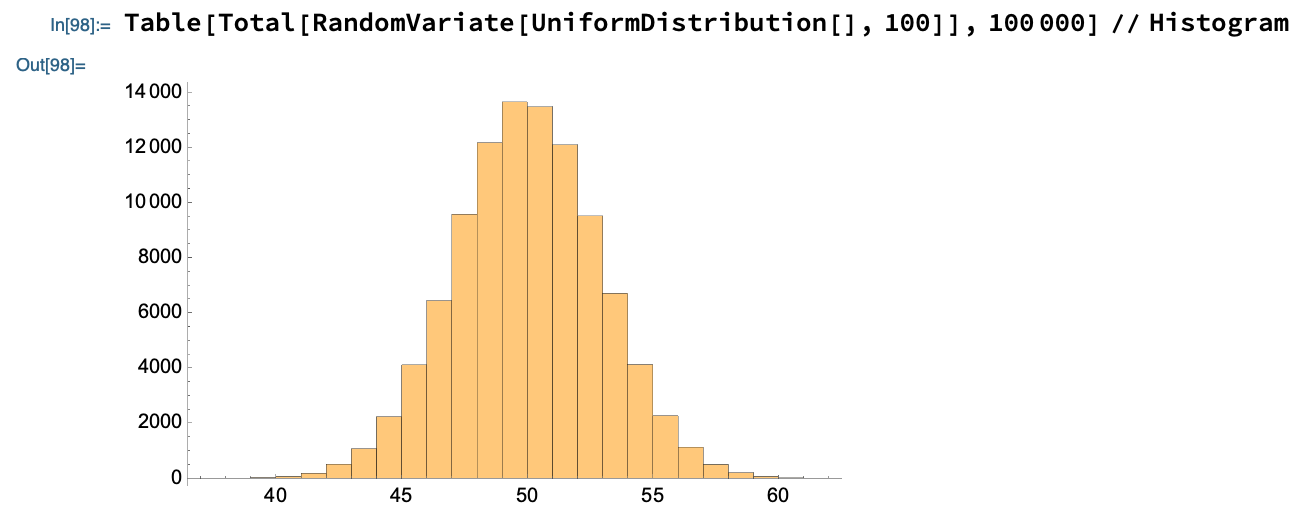
Evidently, the answer tends to be around 45-50ish, but it fluctuates each time we run the computation. To understand the fluctuations, let’s repeat this procedure a large number of times, and look at the histogram of our results.
That’s a Gaussian! And that is the Central Limit Theorem: sums of random variables tend to form a normal distribution when you run the experiment many times. But if this verbiage is confusing, just look at the Mathematica code! That one line contains the heart of the CLT.
People tend to discuss the CLT in terms of averages of the random variable being sampled. But of course, if a sum of random variables is normally distributed, so too will be the average––the average is proportional to the sum!
The only difference is that now we have replaced “Total” with “Mean”. We see a gaussian yet again––a different mean and a different variance, but a gaussian all the same.
Let us now poke and prod at this result from various angles. How robust is it? We made a few choices above. Does this central-limiting behavior depend on any of those choices?
Firstly, we decided to sum up 100 random samples. What happens if we change this number? Let’s use 2, 3, 5, 10, 1000, and 10000 samples, and see what happens.
Evidently, two random samples is not quite enough to get the gaussian distribution. But even with three samples, the distribution is clearly taking shape. So central-limiting behavior appears to be robust to the number of random variables summed.
We also arbitrarily decided to run the experiment 100,000 times and plot a histogram of the results. How does central-limiting behavior depend on the number of trials? We expect that we need a certain minimum number of trials to even know what shape the distribution takes. Let us try powers of 10: 10, 100, 1 000, 10 000, 100 000, 1 000 000, 10 000 000. (We now return to using 100 samples).
Perhaps this is what we should have expected! Below a certain number of trials, it is not at all clear what the distribution will ultimately look like. But around 1000-10000 trials, the distribution is clearly taking shape.
We conclude that above a certain minimum number of samples and trials, we can expect central limiting behavior to emerge, at least for the uniform distribution.
So let us finally turn to the most interesting variable in our experiment: the statistical distribution being sampled. We originally chose a uniform distribution on the interval [0, 1]. What happens when we choose other distributions? As it turns out, some distributions converge much more slowly to central-limiting behavior.
Suppose, to test the dumbest case first, we sample instead from a normal distribution. We would certainly hope that the sums of these random samples are distributed normally. And indeed this is what we observe.
How about discrete distributions? The Bernoulli distribution describes events with only two possible outcomes, one of which has probability p and the other (1 - p). This distribution might describe the outcomes of flipping a (potentially biased) coin. If p = 0.75 and we flip 10,000 coins, we might see a distribution like this.
Does the Bernoulli distribution exhibit central-limiting behavior? It is easy enough to test.
Indeed it does! So the CLT is clearly at least a somewhat robust phenomenon to the choice of statistical distribution.
Now, let’s break it.
To do so, we will use fat-tailed distributions, which Taleb has written about extensively in the Incerto. One example of a fat-tailed distribution is the Pareto distribution, which has a power-law tail.
We can see that for α ~ 1, the tail of this distribution does indeed get long. What does this mean for our samples? Let α = 1.2, which appears to be close to the edge separating fat vs. thin-tailed. We sample this distribution a large number of times.
At first, this seems like a boring histogram with all data concentrated near 0, but if we look closer, we can see that 1 of our 1,000,000 random samples exceeded a value of 10,000! Perhaps you can already see why fail-tailed distributions are a problem for the central limit theorem.
Let’s run our usual experiment again on the Pareto distribution.
That’s not a gaussian! It appears that we get nearly 1,000,000 results clustered near 0, and yet a very small number of sums, just 70, exceed 20,000!
So we can already see that fat-tailed distributions are a different beast. With this number of trials and samples-per-trial, central-limiting behavior had already emerged in every other distribution we have look at thus far. Let us see if increasing both of these numbers allows us to get closer to the normal distribution we expect. Let’s try increasing the number of samples to 10,000 and the number of trials to 10,000,000.
It appears that things are not getting better: we are still nowhere close to the Gaussian we were hoping for! And my computer is really starting to sweat. So, when α is below a certain value, the Pareto distribution does not exhibit central limiting behavior––at least, not without a very large amount of computation. Is this very slow convergence to central-limiting behavior a particular property of the Pareto distribution?
Another fat-tailed distribution is the Cauchy distribution. We determine whether the Cauchy distribution exhibits this same property.
Although the distribution looks bell-shaped, in fact the formula for the PDF is given by
and hence it decays much less quickly with x than the Gaussian does. Let us now perform our central limit test again.
Again, this is nowhere close to a gaussian, even having sampled 10,000,000 times! Almost every sum is approximately zero, except for the one that exceeds 60 million! (With a few in between.)
I could continue along these lines, but I think that the central message should by now be clear. The CLT is a real phenomenon. Central-limiting behavior emerges robustly from a wide variety of statistical distributions––discrete, continuous, finitely supported, infinitely supported––after a non-astronomical number of trials. It is easy to observe this behavior with small computational experiments run on a laptop.
However, there exist distributions that do not practically obey the Central Limit Theorem. These distributions, fat-tailed distributions, have the property that there is a non-negligible (but still small) probability of generating a sample with a very large magnitude. In fact, I believe that these distributions do exhibit central-limiting behavior eventually, but our explorations have revealed that we would need astronomical numbers of trials before we observe this behavior.
The Central Limit Theorem is widely used for statistical inference––for example, when using a sample mean to estimate a population mean. It is thus heartening to know that we can reliably reproduce central-limiting behavior in controlled computer experiments under rather general circumstances. Nevertheless, in real-world experiments, if there is reason to believe a variable is fat-tailed, other techniques will probably have to be used for reliable inference.
I hope that you have found this demonstration illuminating! I certainly learned a lot while exploring these ideas. I should also recommend for the nth time that you read Dr. Taleb’s books.
Thank you for coming to my blog, and I hope I will see you back here soon :)
Until then, be well.
-Matt