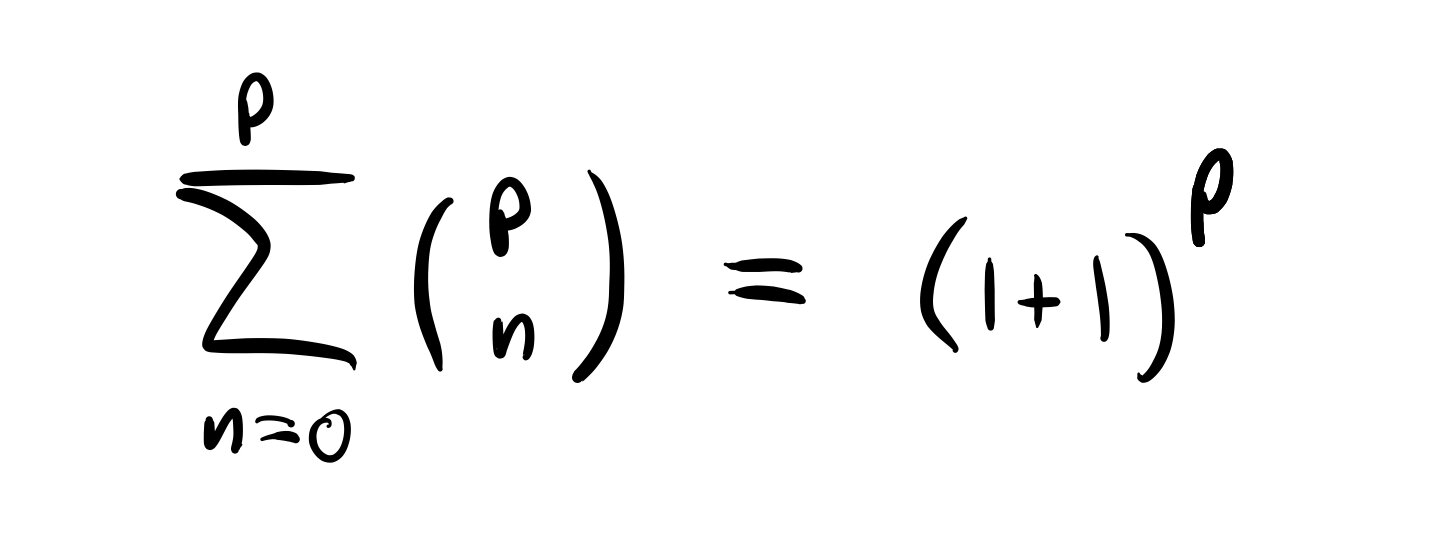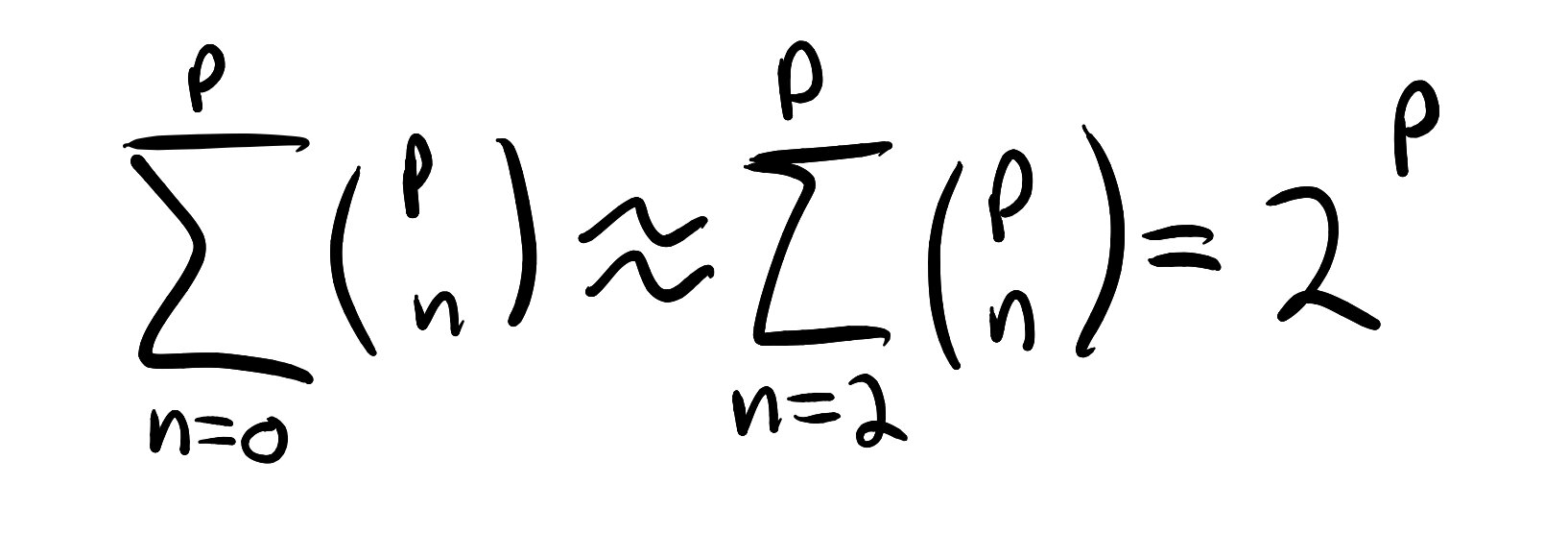Everyone to Everyone — Matthew Kafker

“The fundamental property of the internet, more than any other single thing, is that it connects everyone to everyone.” - Naval Ravikant.

Hello everyone! Welcome to my blog :)

Today, I have a quick back of the envelope calculation to share with you, which has a somewhat surprising result.

Here’s the basic question: how many collaborations between people could the internet possibly facilitate? I was inspired by this quote from Naval Ravikant above to look into this question. The combinatorics are quite straightforward, so it’s not hard to get a numerical answer.

Assumptions: Let’s assume that everyone on Earth has access to the internet. We’ll call the total population P ~ 8 billion. Furthermore, we’ll assume that everyone can, in principle, contact everyone else who is connected to the internet. (Recall, this is a back of the envelope calculation. All models are wrong, some are useful!) We will define a collaboration to be a group of two or more people.

Let’s dive into it.

We’ll do some concrete calculations to get started. How many collaborations are possible between two people on Earth? We can guess that the answer is going to be something like “a lot.” The way you compute it is

where “C” is the number of collaborations. Why? Well, there are P choices for the first person in the collaboration, and P-1 choices for the second. We divide by two since (you, me) is the same collaboration as (me, you). Plugging in numbers, we see that

So there are about 10^19, or 10 quintillion possible two-person collaborations that the internet makes possible. That’s already an enormous number. So how about collaborations of three people?

or 100 octillion. So there are 10 billion times as many three-person collaborations as there are two-person collaborations! These numbers are already ridiculously large, which is just a hint that our total answer is going to be dominated by larger collaborations.

(Why the 6 in the denominator? It’s how many ways you can rearrange/permute a set of 3 objects. Recall that we do not want to count (me, you) differently from (you, me). )

The general formula for the number of collaborations between M people is given by

which is known as the “binomial coefficient.” The exclamation marks refer to factorials. The term P!/(P-M)! will give us P(P-1)(P-2)…(P-(M-1)). The M! in the denominator ensures that we do not count any collaboration multiple times by permuting its members.

We have already seen

But now that we have a general formula, we can start moving towards answering our initial question. First, we should realize that the total number of possible collaborations will be (the number of two-person collaborations) + (the number of three-person collaborations) + … , so we are actually interested in the quantity

Let’s get a feel for the types of numbers involved here. Let’s say, for instance, that you wanted to see how many ten-person startups the internet could possibly facilitate. The answer would be

or 100 novemvigintillion. (Okay, that name is probably not particularly useful to include, but have you ever heard before?? Me neither.)

It is probably worth remembering that the number of atoms in the universe is only ~ 10^79, so there are 10 trillion times the number of possible 10-person startups as there are atoms in the universe. This is number is literally astronomical! And remember that we are going to consider collaborations up to 8 billion people, so we’re really just getting started.

What if you wanted to start a 100-person message board to share old southern pie recipes? Well then, you could construct

such message boards. We’re now firmly beyond the territory where our imagination can be helpful. This number is stupidly large.

Or suppose you wanted to put together a mailing list to distribute your Space-Is-Fake conspiracy newsletter to 10,000 devoted followers? Then you could construct

such mailing lists. Okay, we’re just having fun at this point, but these calculations are really starting to make Mathematica sweat. There is no hope for us to put 8,000,000,000 as the upper bound for that summation and have the computer spit anything out before we’re old. So what can we do?

Well, there is a very useful result in math involving the binomial coefficient which is known as the binomial formula:

In general, this is a useful result for expanding out polynomials. But x and y are simply numbers, so look what happens when we plug in x = y = 1:

Or, in other words,

where we have only made the small approximation of omitting the first two terms of the sum.

But this final equality is precisely what we want! It tells us how to compute the total number of possible collaborations involving at least two people. Plugging in numbers, we get

Take a good look at that last number. Unless you regularly watch Numberphile (which you should certainly do), I can almost promise that that is the biggest number you have ever seen.

In summary, how many collaborations could the internet possibly facilitate, in principle? Well, 10^(30 million) or so.

But why is any of this important? I sincerely believe that there is more to this post than me just writing down very large numbers, and saying “look how ridiculously, gobsmackingly large that number is!”

Because that number of 10^(30 billion) is more than an idle mathematical result. It suggests the potential of the new world that has opened to us with the advent of the internet. Although the everyone-to-everyone approximation that I made to perform these calculations is a bit unrealistic, it gets less so with each passing year. And I believe that this was Ravikant’s point in the quote at the top of this post.

Whether we have realized it or not, the internet has opened up access to a combinatorially enormous space of possible projects, collaborations, businesses, groups, and friendships. We spend a considerable amount of time at one another’s throats, but if we could stop and take stock for a moment, perhaps we would see the universe of possibilities that awaits us at our fingertips at all times.

Think of the technologies that could be found by even partially mining this space of collaborations. The art. The science. The love. The wealth to be found for us all, especially those who need it most.

Sometimes I find it hard to imagine that the future will be good. It can be hard to see where we can go from here as a species. But this little exercise is actually helpful check on that pessimism. I’m not saying that we will necessarily maximize our potential, but there is plenty of room up there for us to get started :)

Thanks for reading my blog!

-Matt

P.S. I originally heard the Ravikant quote in this Meaningwave song by the inimitable Akira the Don.